1. СИСТЕМ ЛИНЕАРНИ РАВЕНКИ СО ДВЕ ПРОМЕНЛИВИ
Конјункцијата од две равенки f (х,у)= 0 и g (x,y)=0 со две променливи, т.е.
f (x,y)=0 ∧ g (x,y)=0 или
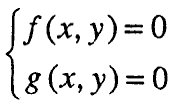
се вика систем равенки со две променливи.
Ако М₁ и М₂ се множествата решенија на равенките f (x,y)= 0 и g (x,y)=0 ,тогаш М₁ ∩ М₂ е множеството решенија на системот равенки. Секој систем од 2 линеарни равенки со две променливи може да се доведе во општ вид:
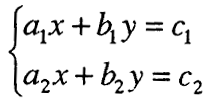
каде што х и у се променливи а a₁, a₂, b₁, b₂, c₁, c₂ се кои било реални броеви или изрази кои не зависат од променливите.
Броевите a₁, a₂, b₁, b₂ се викаат коефициенти пред променливите, а c₁, c₂ – слободни членови на системот.

1.1. Решавање систем линеарни равенки со две променливи
1°. За два система равенки, велиме дека се еквивалентни ако тие имаат еднакви множества решенија.
2°. Ако која било од равенките на даден систем се замени со еквивалентна на неа равенка, се добива систем еквивалентен на дадениот.
3°. Ако од една равенка на системот

едната променлива (на пр. у) може еднозначно да се изрази преку другата променлива: у = g(x), тогаш системот равенки

е еквивалентен со првиот,т.е. (1) <=> (2).
На ова тврдење се базира методот на замена за решавање на систем од две равенки со две променливи.
4°. Системот равенки:

е еквивалентен со системот равенки:
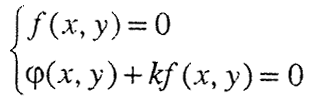
каде што k е кој било реален број. На ова тврдење се базира методот на спротивни коефициенти за решавање на систем од две равенки со две променливи.
1.2. Детерминанти од втор ред и нивна примена
Квадратната шема 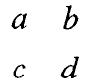 на која и се придружува бројот a d – b c се вика детерминанта од втор ред. Се запишува:
на која и се придружува бројот a d – b c се вика детерминанта од втор ред. Се запишува:

Броевите а и d ја чинат главната дијагонала, а броевите c и b – споредната дијагонала на детерминантата.
Значи, вредноста на детерминантата од втор ред е еднаква на разликата од производите на нејзините елементи од главната и споредната дијагонала.
Системот равенки

под услов a₁ b₂ – a₂ b₁ ≠ 0 има единствено решение (2):
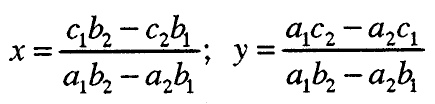
Ако изразите во формулата (2) се означени со детерминантите:

тогаш компонентите на решението на системот (1) може да се запишат во следниов вид:
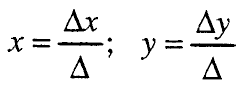
при ∆ ≠ 0 , формулитесе викаат Крамерови формули.
1.3. Дискусија на решенијата на систем линеарни равенки со две променливи
Да се дискутира за решенијата на системот линеарни равенки со две променливи
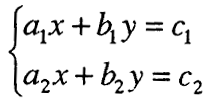
значи да се утврди при кои релации меѓу коефициентите (при претпоставка тие да се различни од нула), тој да има единствено решение, нема решение или има бесконечно многу решенија.
1°. Ако 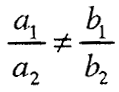 , тогаш системот е решлив, т.е. има единствено решение.
, тогаш системот е решлив, т.е. има единствено решение.
2°. Ако , тогаш системот нема решение, т.е. тој е нерешлив.
, тогаш системот нема решение, т.е. тој е нерешлив.
3°. Ако 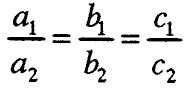 , тогаш системот е решлив и има бесконечно многу решенија.
, тогаш системот е решлив и има бесконечно многу решенија.
1.4. Графичко решавање систем линеарни равенки со две променливи
1) Системот линеарни равенки со две променливи има единствено решение ако графиците на равенките на системот -правите р₁ и р₂ се сечат. Координатите на пресечната точка Ѕ, т.е. Ѕ(х₀ , У₀) е решение на системот равенки.
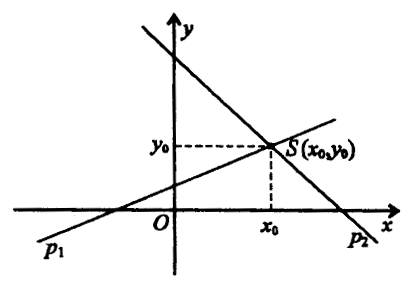
Црт. 1
2) Системот линеарни равенки со две променливи нема решение, ако графиците на равенките на системот -правите р₁ и р₂ немаат заедничка точка, односно кога правите се различни паралелни прави (црт. 2)
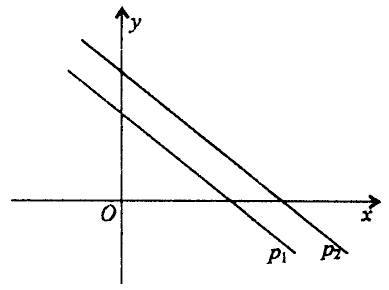
(црт. 2).
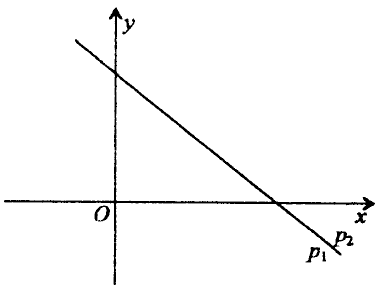
3) Системот линеарни равенки со две променливи има бесконечно многу решенија ако графиците на равенките на системот – правите р₁ и р₂ се паралелни прави што се совпаѓаат
(црт. 3).

2. СИСТЕМИ ОД ТРИ ЛИНЕАРНИ РАВЕНКИ СО ТРИ ПРОМЕНЛИВИ
Конјуикцијата од три линеарни равенки
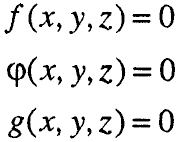
се вика систем од три линеарни равенки со три непознати.
Подредената тројка броеви (x₀,y₀,z₀ ) за која конјункцијата е вистинит исказ е решение на системот равенки.
Секој систем од три линеарниравенки со три променливи може да се доведе во општвид:
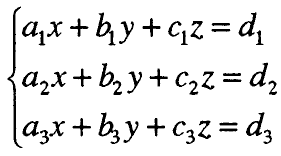
каде х, у, z се променливи.
Броевите аi , bi , сi (i=1,2,3) се викаат коефициенти пред променливите, а d1 (i = 1,2,3) – слободни членови на системот.
2.1. МЕТОДИ ЗА РЕШАВАЊЕ НА СИСТЕМ ОД ТРИ ЛИНЕАРНИ РАВЕНКИ СО ТРИ ПРОМЕНЛИВИ
1) Метод на замена
Една од равенките на системот ја решаваме по која било променлива и со најдениот израз за неа, ја заменуваме соодветната променлива во другите две равенки на системот, со што се добива систем од две равенки со две променливи. По решавањето на добиениот систем, вредностите за двете променливи ги заменуваме во изразот на третата променлива. На тој начин е одредено едно решение на системот.
2) Метод на елиминација
Овој метод ќе го прикажеме на следниов пример.
Пример.
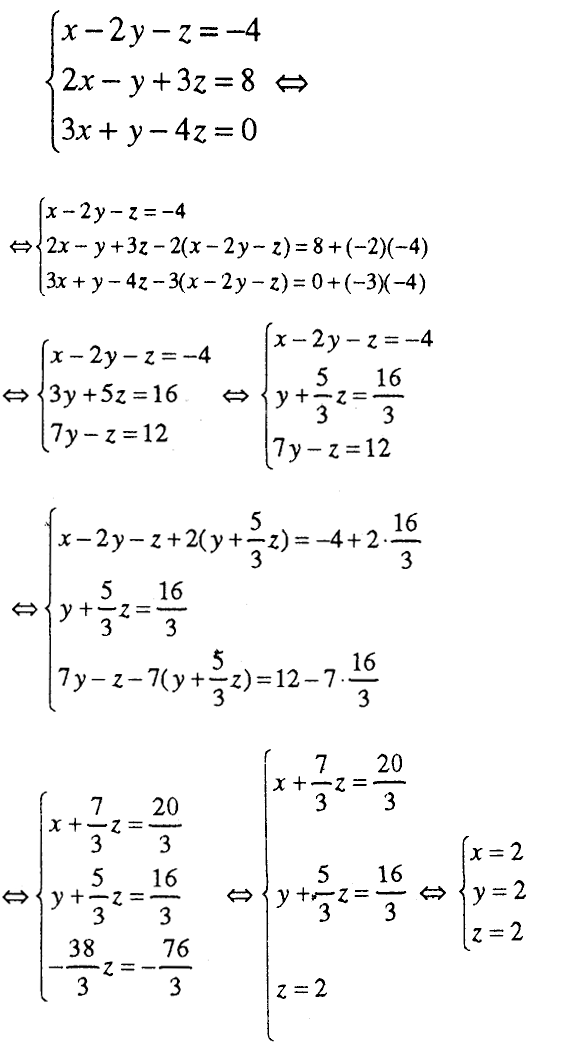
3) Решавање систем од три линеарни равенки со три променливи со детерминанти од трет ред
Квадратната шема  на која и се придружува бројот
на која и се придружува бројот

се вика детерминанта од трет ред, т.е.
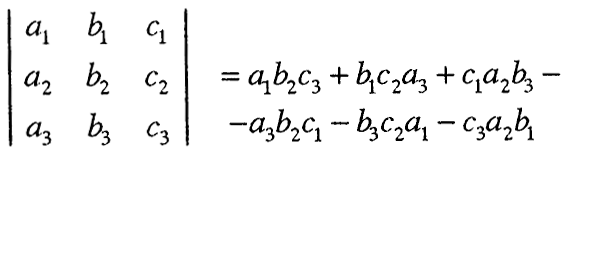
Вредноста на детерминантата може полесно и побрзо да се пресмета со примена на т.н. Сарусово правило, дадено со следнава шема:
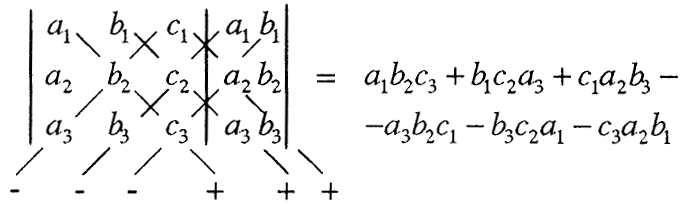
Нека е даден системот равенки:

Може да ги формираме следниве детерминанти:

Ако ∆ ≠ 0 , тогаш за решавањето на системот равенки (1) ги користиме формулите:
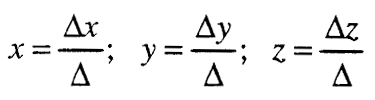
наречени Крамерови формули. При тоа подредената тројка
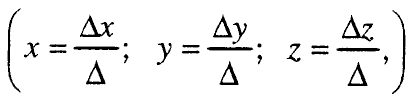
е решение на системот (1).

3. СИСТЕМ ЛИНЕАРНИ НЕРАВЕНКИ СО ЕДНА НЕПОЗНАТА
Конјункцијата на две неравенки А < В и С < D со една непозната, т.е.
(A < B) ∧ (C < D) или ![]() се вика систем од две неравенки со една непозната.
се вика систем од две неравенки со една непозната.
Пример. Да го решиме системот неравенки

Системот го сведуваме на еквивалентниот систем:

Пресекот на множествата решенија на секоја неравенка посебно, т.е.
M = M₁ ∩ M₂
е множество решенија на системот:
M = M₁ ∩ M₂ = ( -∞, – 3/2) ∩ (-3, + ∞) = (-3, – 3/2)
Графички, решението на системот е прикажана на цртежот 1.
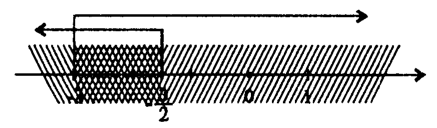
Црт. 1

4. ГРАФИЧКО РЕШАВАЊЕ НА СИСТЕМ ЛИНЕАРНИ НЕРАВЕНКИ СО ДВЕ ПРОМЕНЛИВИ
Под систем линеарни неравенки со две променливи се подразбира конјункцијата од две или повеќе линеарни неравенки со две променливи. Множеството решенија на системот линеарни неравенки е пресекот на множествата решенија на неравенките кои влегуваат во системот. Притоа, ако добиеното множество не е празно, тогаш системот е решлив, а ако пресекот е празно множество -системот е нерешлив.
Пример. Да го решиме графички системот неравенки:
2х-у+4 > 0 ∧ х + у + 2 > 0
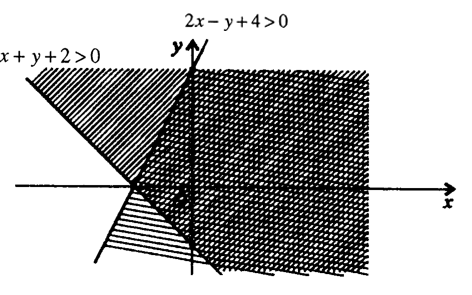
Црт. 2
Двојно шрафираниот дел е решението на системот неравенки.

