1. Квадратни неравенки
Неравенката од видот:
аx² + b + c > 0 или ах² + bx + c < 0
односно
аx² + bx + c ≥ 0 или аx² + bx + c ≤ 0
каде што а, b, c се реални броеви и а ≠ 0 се вика квадратна неравенка со една променлива.
Решавањето на една од квадратните неравенки аx² + b + c > 0 или аx² + b + c < 0
се сведува на одредување на оние вредности на x , за кои соодветната квадратна функција
f (x) = аx² + bx + c
добива позитивна, односно негативна вредност.
Множеството решенија на неравенката
аx² + bx + c ≥ 0 или аx² + bx + c ≤ 0
ги содржи нулите на соодветната квадратна функција
Пример. Да ја решиме неравенката х² – 2x -3 < 0
Соодветната квадратна функција е f(x) = х² – 2х – 3. Го скицираме нејзиниот график со помош на нејзините нули, што се решенија на равенката х² – 2х – 3. Тоа се броевите х₁=-1 и х₂ =3
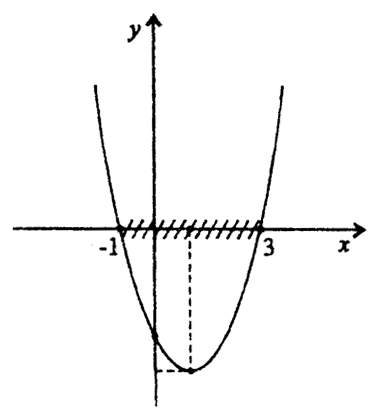
(црт.1).
Од графикот гледаме дека таа е негативна, т.е. графикот е под х-оската, за вредности на х од интервалот (-1 , 3).
2. СИСТЕМ КВАДРАТНИ НЕРАВЕНКИ
Општиот вид иа систем од квадратни неравенки со една променлива е:

Наместо знакот “>“ во неравенките може да стои или ”<“,или “≤“, или “≥“.
Ако М₁ и М₂ се множествата решенија на првата, односно втората неравенка, тогаш множеството решенија М на системот е пресекот на тие множества, т.е.
M = M₁ ∩ M₂

