Спротивниот број на природниот број a се означува со -a.
Множеството од сите природни броеви, нулата и спротивните на природните броеви се вика множество на целите броеви и се означува со Z, т.е.
Z = { …,-3 , -2 , -1 , 0 , 1 , 2 , 3 , … }
Елементите -1, -2, -3, … се негативни цели броеви, а природните броеви 1, 2, 3, … се позитивви цели броеви. Нулата не е ни позитивен ни негативен број.
Апсолутна вредност на цел број a, што се означува со | a |, е сaмиот број aко тој е позитивен или нула, а е спротивен број ако дaдениот е негативен, т.е.
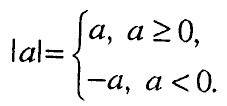
1. ОСНОВНИ ПРАВИЛА ЗА СМЕТАЊЕ СО ЦЕЛИ БРОЕВИ
1.1. СОБИРАЊЕ
Ако a,b ∈ No, тогаш:
1. -(-a) = a; -(+a) = –a
2. (+a)+(+b) = +(a+b)
3. (-a)+(-b) = -(a + b)
4. (+a)+(-b) = +(a – b), за a > b
5. (+a)+(-b) = -(b – a), за a < b
_____________________________________
1.2. МНОЖЕЊЕ
Ако a,b ∈ No, тогаш:
1. (+a) · (+b) = +(ab)
2. (-a) · (-b) = +(ab)
3. (-a) · (+b) = -(ab)
______________________________________
1.3. ОДЗЕМАЊЕ И ДЕЛЕЊЕ НА ЦЕЛИ БРОЕВИ
Разликата на кои било два цели броја е цел број, т.е.
(∀a,b ∈ Z) (a-b) ∈ Z
Oдземањето на цели броеви се дефинира со помош на собирањето. т.е.
(∀a,b ∈ Z) a-b = a +(-b)
За дадени цели броеви а и b, количникот а:b не секогаш
е определен во Z, т.е. не е цел број.
_____________________________________
1.4. КОНГРУЕНЦИИ
Нека a, b се цели броеви и m е природен број. За a и b се вели дека се конгруентни по модул m, ако a и b при делењето со m имаат исти остатоци, т.е. a = mq₁ + r и b = mq₂ + r. Симболички конгруенцијата се означува на следниов
начин:
a ≡ b (mod m)
Пример. 42 ≡ 98 (mod 4)
=>
42=4·10+2 и 98=4∙24+2
____________________________________
1.5. ОПЕРАЦИИ. ГРУПОИДИ
Некa G е дaдено непразно множество. Операција во Множеството G е некое правило или знкон * според кој на секој подреден пар елементи x,y ∈ G му се придружувa точно по еден елемент
Z ∈ G, т.е. x * y = z
Секое непразно множество G, заедно со некоја негова операција * се вика групоид и се запишува (G , *)
Пример 1.
( N , + ); ( N , ∙ ); ( Z , – ) се групоиди, а ( N, – ); (Z , : ) не се групоиди.
За еден групоид ( G , * ) се вели дека:
– е комутативен ако * е комутативна операција, т.е. х * у = у * х, за кои било x,y ∈ G
– е асоцијативен (или е подгрупа), ако * е асоцијативна операција, т.е. (x * y) * z = x * (y * z), за кои било х,у,z∈G.
-има неутрален елемент, ако постои елемент е ∈ G таков што х * е = е * х = е
-има инверзен елемент ако за секој х ∈ G , постои x’ ∈ G, таков што х * х’ = х’ * х = е (елементот х се вика инверзибилен).
____________________________________________
1.6. ГРУПА
Групоидот ( G , * ) е група, ако ги исполнува условите:
1″ (G₁) (G , *) е асоцијативен групоид, т.е. полугрупа;
2″ (G₂) (G , *) има неутрален елемент;
3″ (G₃): Секој елемент во (G , *) има инверзен елемент;
4″ (G₄): Ако групоидот (G , *) е комутативен, тогаш (G , *) се вели дeка е комутативна група или абелова група.
– Celi broevi –

