1. Дефинициона област на тригонометриските функции
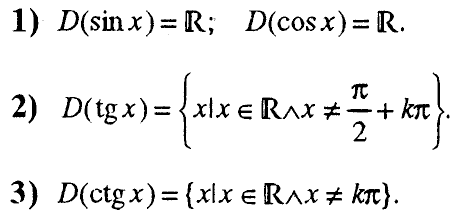
2. Множество вредности на тригонометриските функции

3. Периодичност на тригонометриските функции
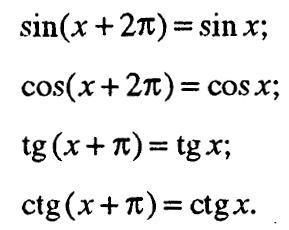
Функциите y = sin x и у = соѕ х имаат период еднаков на 2π, а функциите у = tg x и у = ctg x имаат период π, т.е.Забелешки:
1″. Функциите у = asin x и y = aсоѕ х (a≠0) имаат период од 2π, a функциите у=atg x и у=actg х имаат период π.
2″. За кој и да било реален број с, функциите y=sin(x+c) и y=cos(x+c) имаат период 2π, а функциите y=tg(x+c) и y=ctg(x+c) имаат период π.
3″. За кој и да било број b≠0, периодот на функциите y=sinbx и y=cosbx e 2π⁄b, а на функциите y=tgbx и y=ctgbx е π/b
4″. Функциите у=asin(bx+c) и y=acos(bx+c) имаат период 2π/b а функциите у=atg(bx+c) и у=actg(bx+е) имаат период π/b
4. Парност и непарност на тригонометриска функција
Функциите sin α, tg α и ctg α се непарни функции, а функцијата соѕ α е парна, т.е.
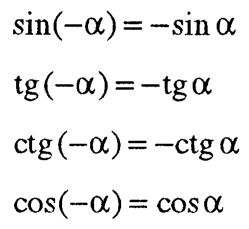
4. Менување на тригонометриските функции
Менувањето на тригонометриските функции е дадено во следнава табела:
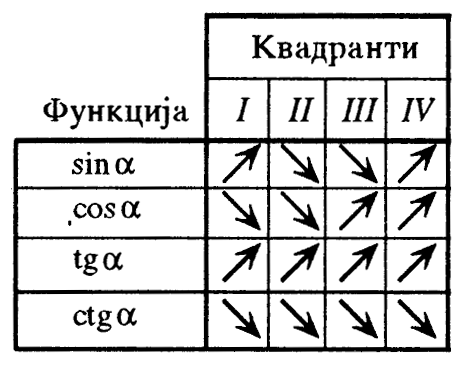
Функцијата у = ѕiп х монотоно расте од интервалот:
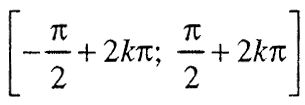
а монотоно опаѓа од интервалот:
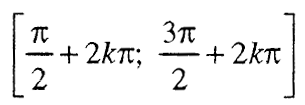
Функцијата у = соѕ х монотоно опаѓа од интервалот:
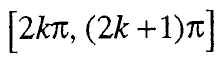
а монотоно расте од интервалот:
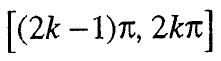
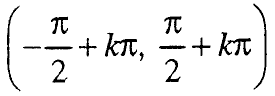
Функцијата у = tg x монотоно расте од -∞ до +∞ на секој интервал и од нив се состои нејзината дефинициона област.
Функцијата у = ctg x монотоно опаѓа од +∞ до -∞ на секој интервал (kπ,(k+1π)) , од кои се состои нејзината дефинициона област.
– osnovni svojstva na trigonometriski funkcii –

