Равенката од видот
ах² + bx + c = 0
каде што х е променлива, а a , b и c (a ≠ 0), се дадени реални броеви се вика квадратна равенка со една променлива.
Равенката е општ вид на квадратна равенка. Ако во неа a = 1, тогаш таа е во нормален или сведен вид и се запишува:
x² + px + q= 0
Ако во равенката ax² + bx + c = 0 коефициентите а, b и c се различни од нула, тогаш равенката се вика полна квадратна равенка, а ако барем еден од коефициентите b или c е еднаков на нула – неполна квадратна равенка.
Неполни квадратни равенки се равенките:
ax² + bx = 0 , c = 0;
ax² + c = 0 , b = 0;

1. РЕШАВАЊЕ НА НЕПОЛНИ КВАДРАТНИ РАВЕНКИ
1. Равенката од видот ax² + bx = 0, а ≠ 0, се решава со разложување на нејзината лева страна на множители, т.е.
x (ax + b) = 0,
а таа е еквивалентна со вкупноста равенки:
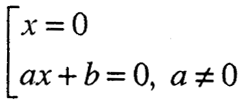
Оттука се добива дека равенката ax² + bx = 0 има две решенија:
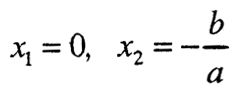
па велиме дека х₁ =х₂ = 0 е двократен корен на равенката aх² = 0.
2. Равенката од видот
ах² + c = 0, a ≠ 0
се решава со префрлање на c на десната страна и делење на двете страни со a, при што се добива:
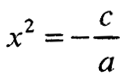
– Ако – c/a > 0 ,т.е. кога a и c имаат различни знаци, равенката има два различни корени:
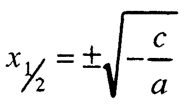
– Ако – c/a < 0 , т.е. кога a и c имаат еднакви знаци, корените на равенката се конјугирано комплексни броеви:
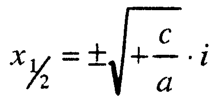

2. РЕШАВАЊЕ НА ПОЛНА КВАДРАТНА РАВЕНКА
Решенијата на полната квадратна равенка
ах² + bx + c = 0
се одредуваат со формулите:

Ако квадратната равенка е дадена во нормален вид
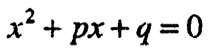
тогаш формулите за корените на равенката го добиваат видот:
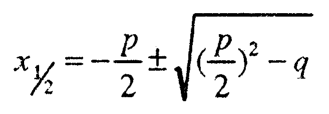
Оваа формула е погодна кога коефициентот р е парен број.

3. ДИСКРИМИНАНТА НА КВАДРАТНА РАВЕНКА
Реалниот број b² – 4ac се вика дискриминанта на квадратната равенка aх² +bx + c = 0 , и се означува со D, т.е.
D = b² – 4ac
Во зависност од знакот на D, може да се одреди природата на решенијата на квадратната равенка aх² + bx + c = 0 (∀a, b, c ∈ R) и a ≠ 0
Решенијата (корените) на квадратната равенка се:
1) реални и различни, ако D > 0
2) реални и еднакви, ако D = 0
3) конјугирано комплексни, ако D < 0

4. ВИЕТОВИ ФОРМУЛИ
Броевите x₁ и х₂ се корени на квадратната равенка
ах² + bx + c = 0
ако и само ако важат равенствата:
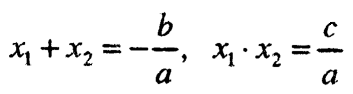
Овие равенства се познати како Виетови формули.
Ако квадратната равенка е дадена во нормален вид:
х² + px + q = 0,
тогаш Виетовите формули се:
х₁ + х₂ = -р
х₁ • х₂ = q

5. РАЗЛОЖУВАЊЕ НА КВАДРАТЕН ТРИНОМ НА ЛИНЕАРНИ МНОЖИТЕЛИ
Изразот ах² + bx + c се вика квадратен трином по однос на променливата х, каде што a,b,c ∈ R и a ≠ 0.
Корените на квадратната равенка ax² + bx + c = 0 се нули на квадратниот трином.
Квадратниот трином ax² + bx + c може да се разложи на линеарни множители со реални коефициенти, т.е.
ax² + bx + c = a (x – x₁) (x – x₂)

