1. ПОИМ ЗА ЛОГАРИТАМ
Логаритам за даден позитивен број b за дадена основа а, а >0 и а ≠ 1, е показател c со кој треба да се степенува основата а за да се добие бројот b, т.е.
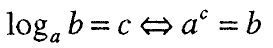
Притоа, b се вика нумерус или логаритманд, а -основа на логаритмот и c – логаритам од b за основа а.
Од дефиницијата за логаритам следува равенството:

кое се нарекува основен идентитет во теоријата на логаритмите.
Непосредно од дефиницијата на логаритам следуваат следниве особини (а > 0 и а ≠ 1 ):
1°. logₐ1= 0 , бидејќи а⁰= 1
2°. logₐа=1, бидејќи а¹=а
3. logͣaⁿ= n, бидејќи aⁿ=aⁿ

2. ПРАВИЛА ЗА ЛОГАРИТМИРАЊЕ
2.1. Логаритам на производ
Логаритмот на производот од позитивните броеви А и В за дадена основа а (а > 0 и а ≠ 1 ) е еднаков на збирот од логаритмите на множителите за истата основа т.е.
logₐAB = logₐA + logₐB
2.2. Логаритам на количник
Логаритмот на количник од позитивните броеви А и В за дадена основа а (а > 0 и а ≠ 1 ) е еднаков на разликата од логаритмот на броителот и логаритмот на именителот за истата основа, т.е.
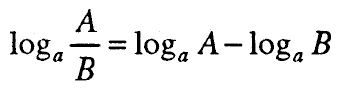
2.3. Логаритам на степен
Логаритам на степен со позитивна основа а, а ≠1, еднаков на производот од показателот на тој степен и логаритмот на неговата основа, т.е.
logₐAⁿ = nlogₐA
2.4. Логаритам на корен
Логаритам на корен од позитивен број е еднаков на количникот од логаритмот на поткореновата величина и показателот на коренот, т.е.
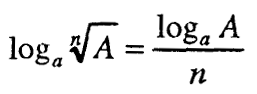

3. ВРСКА MEЃУ ЛОГАРИТМИТЕ СО РАЗЛИЧНИ ОСНОВИ
Нека се а , b и c реални позитивни броеви и нека b и c ≠ 1.
Формулата
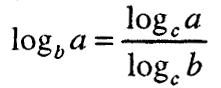
ја дава врската меѓу логаритмите на бројот а при различните основи b и c.
![]()
4. ЛОГАРИТМИРАЊЕ И АНТИЛОГАРИТМИРАЊЕ НА ИЗРАЗИ
Логаритмирање на некој алгебарски израз се врши врз основа на правилата за логаритмирање на произврд, количник, степен и корен и својствата на логаритмите.
Изнаоѓањето на алгебарскиот израз, чиј логаритам е познат, се вика антилогаритмирање.
– logaritmiranje –

