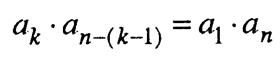Секое пресликување на множеството N на природните броеви во множеството R на реалните броеви се вика низа од реални броеви.
Во низата ![]() членот се вика n-ти член или оnшт член на низата, а a₁-прв, a₂-втор и.т.н.
членот се вика n-ти член или оnшт член на низата, а a₁-прв, a₂-втор и.т.н.
Својства на низите:
1) Moнотони низи.
За една низа ![]() велиме дека расте ако
велиме дека расте ако
(∀n ∈ N) a-n ≤ a-n+1
Слично, низата опаѓа, ако и само ако
(∀n ∈ N) a-n ≥ a-n+1
Ако се испушти знакот за еднаквост, низата строго расте (опаѓа).
Низите што растат и опаѓаат се викаат монотони низи.
Критериум за одредување на монотоност на низа:
1. ![]() или
или  тогаш низата расте
тогаш низата расте
2. ![]() или
или ![]() тогаш низата опаѓа
тогаш низата опаѓа
Пример. Низата со општ член:

опаѓа, бидејќи

2) Ограничени низи
За низата ![]() велиме дека е ограничена ако постои еден број М таков што ниеден член од низата по апсолутна вредност да не го надминува бројот М, т.е.
велиме дека е ограничена ако постои еден број М таков што ниеден член од низата по апсолутна вредност да не го надминува бројот М, т.е.

Низата што не е ограничена се вика неоrраничена.
1. АРИТМЕТИЧКА ПРОГРЕСИЈА
Под аритметичка прогресија подразбираме низа кај која што,почнувајќи од вториот член, разликата меѓу секој член и неговиот претходник е постојана, т.е. за низата ![]() имаме
имаме

Бројот d се вика разлика на аритметичка проrресија. Ако d > 0 , тогаш низата расте. Ако d < 0,тогаш аритметичката прогресија опаѓа. Ако d = 0,тогаш прогресијата ниту расте ниту опаѓа, т.е. сите членови се меѓусебе еднакви. Општиот член на аритметичката проrресија се добива со формулата

Пример. Десетиот член на аритметичката прогресија 3 , 8 , 13 , 18 ,…, т.е.
a₁= 3 , d=5 , n=10
a₁₀ = a₁ + (10-1)d = a₁ + 9d = 3+9∙5=48
1.1. Некои својства на членовите на аритметичка прогресија
1°. Во една аритметичка проrресија со конечен број членови,збирот на два члена еднакво оддалечени од крајните членови е еднаков на збирот од крајните членови,т.е.

2°. Секој член на една аритметичка проrресија (освен првиот) е аритметичка средина на неговите два соседни членови, т.е.

Важи и поопшто дека:

3. Средниот член на една аритметичка проrресија со непарен број членови е еднаков на обопштената аритметичка средина од останатите членови, т.е.

1.2. Збир на првите n-членови на една аритметичка прогресија
Збирот напрвите n-членови на една аритметичка прогресија е еднаков на

Ако во оваа формула се внесе вредноста на

се добива

Пример. Збирот на првите 12 членови на аритметичката прогресија

2. ГЕОМЕТРИСКА ПРОГРЕСИЈА
Низа од броеви кај која количникот меѓу секој член,освен првиот,и неговиот претходник е константен број се вика геометриска прогресија.
За низата a₁ , a₂ ,…, an , ….. имаме an : an-1, (q=константа). Бројот q се вика количник на геометриската прогресија.
Ако q>1, тогаш геометриската прогресија за а₁>0 монотоно расте, а при a₁<0 монотоно опаѓа.
Ако 0 < q < 1 и a₁ < 0, прогресијата монотоно расте, а ако a₁ > 0 монотоно опаѓа.
Ако q < 0, членовите на прогреснјата алтернативно се менуваат како позитивни и негативни, и тоа се вика алтернативна геометриска прогресија.
Ако q = 1, сите членови на прогресијата се еднакви, т.е. таа е “константна” прогресија.
Општиот член на геометриската прогресија се добива со формулата:

Пример. Да го определиме седмиот член на геометриската прогресија 2 , 6 , 18 , 54 , …
Решение.
a₁ = 2, q = 3 и n = 7
Од формулата ![]() имаме:
имаме:

2.1. Некои својства на членовите на геометриска прогресија
1) Производот на два члена од една геомериска прогресија, еднакво оддалечени од крајните членови на прогресијата, е еднаков на производот од крајните членови, т.е.
2) Секој член на една геометриска прогресија (освен првиот) е геометриска средина на двата соседни члена, т.е.

3) Во секоја rеометриска прогресија a₁ , a₂ , … an-1 за секој n ≥ 1 важи:

2.2 збир од првите n-членови на геометриска прогресија
Збирот од првите n членови на геометриска прогесија се определува со формулата:

Пример: Да го пресметаме збирот од првите шест членови на геометриската прогресија 2 , 6 , 18,…
Решение.
a₁= 2 , q =3 и n=6
Заменувајќи ги овие вредности во формулата за збирот, се добива: