1. СТЕПЕН СО ПОКАЗАТЕЛ ПРИРОДЕН БРОЈ
Нека a e реален број, а n природен број. Производот a · a · a · …· a = aⁿ
сe вика n-ти степен на бројот a.
Симболот aⁿ се вика стeпен, бројот a основа на степенот, n– степенов показател или експонент. Степенот на бројот a со експонент 1 е самиот број a, т.е.
a¹ = a
2. СТЕПЕН СО ПОКАЗАТЕЛ ЦЕЛ БРОЈ
Степенсо показател 0 е еднаков на 1, т.е. a⁰ = 1
Степен со показател цел неrативен број е:

3. ПОЛИНОМИ. РАЦИОНАЛНИ ИЗРАЗИ
Изрази формирани со помош на константи и променливи, користејќи ги операциите собирање, одземање, множење и делење на реални броеви, како и степенување со показател природен број, се викаат рационални алгебарски изрази. Изрази, формирани како производ од некоја константа и степените од некоја променлива се викаат мономи. Мономот е даден во нормален вид, ако тој содржи само еден броен множител и не содржи степени со иста основа.
– За мономот 2х²у³, бројот 2 се вика коефициент на мономот, а другиот дел главна вредност.
– Мономи што имаат исти главни вредности се викаат слични.
– Степен на моном е збирот од показателите од степените на променливите во тој моном.
– Збир од конечен број мономи се вика цел рационален израз или полином.
– Изрази во кои се јавува делење со променлива или со израз што содржи променливи, се викаат дробно рационални изрази.
– Најголемиот од степените на мономите што го сочинуваат полиномот се вика степен на полиномот.
4.1. Квадрат на бином
(А + В)² = А² + 2АВ + В²
(А – В)² = А² – 2АВ + В²
4.2. Производ од збир и разлика на два изрази
(А + В)·(А – В) = А² – В²
4.3. Трет степен на бином
(А + В)³ = А³ + ЗА²В + 3АВ² + В³
(А – В)³ = А³ – 3А²В + 3АВ² – В³
4.4. Делење на полином со моном
Полином се дели со моном на тој начин што секој член од полиномот се дели со мономот.
Пример:
(12х²у³ + 8x⁴y⁶) : 4xy² = 3xy + 2x³y⁴
4.5. Делење на полином со полином
Постапката за делење на два полинома се состои во следново:
– деленикот и делителот се подредуваат по експонентите на една од променливите што влегуваат во нив
(од најголема кон најмала);
– првиот член од деленикот се дели со првиот член од делителот и се добива првиот член од количникот;
– првиот член од количникот се множи со делителот и добиениот производ се одзема од деленикот;
– првиот член од првиот остаток се дели со првиот член од делителот и се добива вториот член на количникот. Постапката продолжува се додека не се добие остаток нула или остаток чиј степен по таа променлива е помал од степенот на делителот по истата променлива.
Пример.
(5х³ – 8х² + х – 3) : (х² – 2) = 5х – 8
±5х³ + 10х
___________
-8х² + 11х – 3
+8х2 ± 16
_________
11х – 19
Количникот од делењето е полиномот 5х – 8, а 11x – 19 е остатокот.
5. РАЗЛОЖУВАЊЕ НА ПОЛИНОМИ НА МНОЖИТЕЛИ
5.1. Разложување со извлекување заеднички множител пред заграда
АХ + ВХ = Х(А + В)
5.2. Разложување со примена на формулите за скратено множење
1. А² – В² =(А – В)·(А + В)
2. А² ± 2АВ + В² = (А ± В)²
3. А³ ± В³ = (А ± В)·(А² -+ АВ + В²)
5.3. Разложување со групирање на членовите
Со овој начин на групирање ќе се запознаеме преку следниов пример:
х² – 3х – y² + Зу =
= (х² – y²) – (Зх – Зу) =
= (х – у) · (х + у) – З(х – у) =
= (х – у) · (х + у – 3)
6. НАЈГОЛЕМ ЗАЕДНИЧКИ ДЕЛИТЕЛ (НЗД)
Заедничкиот делител на два или повеќе полиноми што ги содржи сите нивни заеднички делители се вика најголем заеднички делител (НЗД) на тие полиноми.
НЗД на два или повеќе полиноми го наоѓаме на следниов начин:
– дадените полиноми ги разложуваме на прости множители;
– се множат меѓусебно сите прости множители што се заеднички за дадените полиноми и при тоа секој од нив се зема со најмалиот показател со кој се јавува во разложените полиноми.
Пример 2. Да го најдеме НЗД на полиномите:
2a² – 2ab и 8a² -8b²
2a² – 2ab = 2a ·(a – b);
8a² – 8b² = 8(a² – b²) = 2³(a – b)(a + b)
значи НЗД на 2a² – 2ab и 8a² – 8b² = 2(a – b)
Полиномите што немаат друг заеднички делител освен бројот 1 се викаат заемно прости полиноми.
7. НАЈМАЛ ЗАЕДНИЧКИ СОДРЖАТЕЛ (НЗС)
Содржател што е делител на сите други содржатели, се вика најмал заеднички содржател (НЗС) на дадените полиноми.
НЗС на два или повеќе полиноми го наоѓаме на следниов начин:
– дадените полиноми се разложуваат на прости множители;
– потоа се образува производ од сите прости множители и притоа секој од нив се зема со најголемиот показател со кој се јавува во разложените полиноми.
Пример 2. Да го најдеме НЗС за полиномите:
x² – y²; x³ – y³; x² – 2xy + y²;
решение:
x² – y² = (x – y)(x + y)
x³ – y³ = (x – y)(x² + xy + y²)
x² – 2xy + y² = (x – y)²
значи НЗС за сите изрази е: (x + y)(x – y)²(x² + xy + y²)
АЛГЕБАРСКИ ДРОПКИ
Изразот А/B, кадешто А , В ≠ 0 се полиноми, се вика алгебарска дропка. А се вика броител, а В именител на дропката.
8.1. Проширување на алгебарска дропка

8.2. Скратување на алгебарска дропка
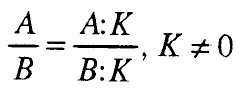
9. ОПЕРАЦИИ СО АЛГЕБАРСКИ ДРОПКИ
9.1. Собирње и одземање
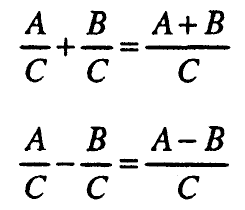
9.2. Множење
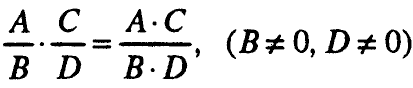
9.3. Делење
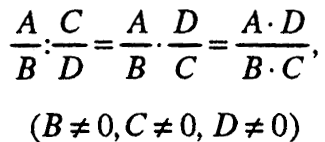
9.4. Двојни алгебарски дропки

– Algebarski racionalni izrazi –

