Равенката од видот:
ах² + bxy + c + dx + ey + f = 0
е општ вид на квадратна равенка со две променливи, при која барем еден од коефициентите пред квадратните членови а, b и c е различен од нула.
Системот:
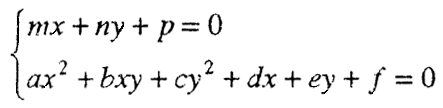
е општ вид на систем од една линеарна и една квадратна равенка со две променливи. Ваков систем се решава со методот на замена, имено, од линеарната равенка ја изразуваме едната од променливите и ја заменуваме во квадратната.
Пример. Да го решиме системот равенки:
2x + y = 1
x² +xy + y² = 1
Ја изразуваме променливата у од првата равенка:
у = 1 – 2х
па со замена на у во втората равенка со изразот
1 – 2x
се добива:
х² + x(1 – 2х) + (1 – 2х)² = 1
откако ќе се реши се добива Зх² – Зх = 0, т.е 3x(x – 1) , чии корени се х₁ = 0, х₂ = 1.
Заменувајќи ги овие вредности на х во равенката у = 1 – 2х, се добиваат соодветните вредности за у, т.е. y₁ = 1, y₂ = -1.
Значи, решенијата на системот се подредените двојки броеви (0 , 1) и (1 , -1).

