1. Општ вид равенка на права
Равенката од видот: Ax + By + C = 0 се вика општ вид равенка на права.
Својства:
1. Ако А = О, се добива равенката By + C = 0, односно y = – C/B, што претставува права, паралелна со х– оската, на растојание – C/B од координатниот почеток.
2. Ако В = О, равенката се сведува на Ax + C = 0, односно x = – C/A што претставува права, паралелна со у-оската, на растојание – C/A од координатниот почеток.
3. Ако B= 0, C = 0, равенката на права се сведува на видот Ax=0, односно x=0. Таа се совпаѓа со y-оската и претставува нејзина равенка.
4. Ако А = 0, С = 0, равенката на права се сведува на видот By = 0, односно y=0. Правата се совпаѓа со х-оската и претставува нејзина равенка.
2. Експлицитен вид равенка на права
Равенката у = kx + b , каде што k = tg а, се вика равенка на права во експлицитен вид (црт. 4).

Црт. 4
Бројот k се вика коефициент на правецот на правата, а b-отсечок што правата го отсечува на у-оската.
3.Сегментен вид равенка на права
Равенката на права во сегментен вид е:
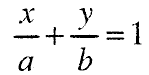
во која а и b се отсечоци што правата ги отсечува на координатните оски х и у, соодветно (црт. 5).
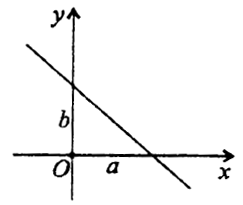
Црт.5
4. Нормален вид равенка на права
Нормалниот вид на равенка на правата што е дадена во општ вид е

во која знакот пред коренот е спротивен на знакот пред коефициентот С.
5. Равенка на права низ една и две точки
Равенката на права што минува низ дадена точка М (x₁,y₁) и има коефициент на правец k гласи:
y – y₁= k (x – x₁)
Равенката на права што минува низ две дадени точки М₁(x₁,y₁) и M₂ (x₂,y₂) го има следниов вид :

6. Растојание од точка до права
Растојанието од точката M (x₀,y₀) до правата Ax + By + C = 0 се пресметува по формулата :
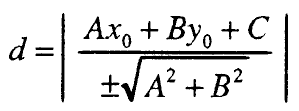
7. Агол меѓу две прави
Аголот меѓу правите l₁, и l₂ (црт.б) се одредува по формулата:
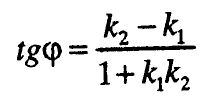
каде што k₁, и k₂ се коефициенти на правците на правите l₁ и l₂, соодветно.
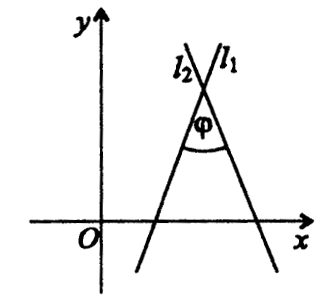
Црт. 6
Од формулата (1) се добиваат условите за паралелност и нормалност на две прави. Така, l₁||l₂, ако k₂= k₁, l₁⊥l₂ ако 1 + k₁k₂=0

