1. ПОИМ ЗА ЛИНЕАРНА РАВЕНКА
Ако А и В се алrебарски изразии ако барем едниот од нив содржи променлива, тогаш формулата (равенството) А = В се вика алгебарска равенка; за променливите се вели дека се непознати во равенката. Една алгебарска равенка може:
– да има решение, т.е. е решлива равенка, ако нејзиното множество решенија не е празнo множество;
– да нема решение, т.е. е нерешлива равенка ако нема ниту едно решение.
За две равенки А = В и C = D се вели дека се еквивалентни равенки ако нивните множества решенија се совпаѓаат. Се означува: (A=B <=> C = D) <=> M₁= M₂
каде што М1 е множеството решенија на равенката А=В, а М₂ на равенката C=D.

2. ЛИНЕАРНИ РАВЕНКИ СО ЕДНА НЕПОЗНАТА
Ако во алгебарската равенка А = В по нејзиното средување непознатата х се јавува само со прв степен, тогаш за таа равенка се вели дека е линеарна равенка. Секоја линеарна равенка може да се доведе во обликот ах+b = 0 , каде што а и b се некои реални броеви. Равенката ax + b = 0, во случај кога:
1°. а ≠ 0, таа е решлива и има само едно решение: – b/a
2°. а=0 ∧ b=0, Таа е исто така решлива, т.е. секој реален број е нејзино решение, т.е има бесконечно многу решенија
3°. а=0 ∧ b ≠ 0, равенката е нерешлива, бидејќи равенката 0•х + b = 0, b ≠ 0, не станува точно бројно равенство за ниеден реален број х.

3. ЛИНЕАРНА РАВЕНКА СО ДВЕ НЕПОЗНАТИ
Секоја алгебарска равенка што може да се доведе во обликот:
ax + by = c (1)
каде што а, b, c се реални броеви се вика линеарна равевка со две променливи (непознати) х и у. Броевите а и b се коефициенти пред непознатите, а c – слободен член на равенката.
Решението на равенката (1) е секој подреден пар реални броеви (хₒ,уₒ) за кој таа преминува во точно равенство.
Равенката ax + by = c, во случај кога а ≠ 0 или b ≠ 0 има бесконечно многу решенија
Во случај кога а=0 и b=0, равенката ax + by = c е од обликот 0x + 0y = c и за:
- c ≠ 0 таа е нерешлива и М е празно множество,
- c = 0 таа е решлива и има бесконечно многу решенија (M = R x R).
Графичкиот приказ на линеарна равенка со две променливи е права.

4. ЛИНЕАРНА НЕРАВЕНКА СО ЕДНА НЕПОЗНАТА
Ако два алгебарски изрази А и В (кои се со по една променлива) се сврзат со еден од знаците за неравенство <,≤, > или ≥ (пример: А < В), тогаш се добива предикат со една променлива што се вика неравенка со една непозната.
Неравенките А < В и С < D се еквивалентни ако множеството решенија е еднакво со множеството решенија на другата неравенка, т.е
A < B <=> C < D
Својства на неравенките
– A < B <=> B > A
– А < B <=> A + C < B + C – C > 0 => (A < B <=> AC < BC)
– C < 0 => (A < B <=> AC > BC)
Секоја неравенка која може да се доведе во обликот ах < b, каде што а и b се реални броеви, се вика линеарна неравевка со една непозната.

5. ГРАФИЧКО РЕШАВАЊЕ НА ЛИНЕАРНИ НЕРАВЕНКИ СО ДВЕ ПРОМЕНЛИВИ
Неравенката од облик:
ax + by + c > 0, или ax + by + c < 0, односно ax + by + c ≥ 0, или ax + by + c ≤ 0, каде што a,b,c ∈ R, а х и у се променливи, се вика линеарна неравенка со две променливи. Решенијата на линеарна неравенка со две променливи е множеството точки од една полурамнина.
Пример 1. Множеството решенија на неравенката 2х – у + 4 > 0
графички е одредено на цртежот 1 со полурамнината шрафиран дел.
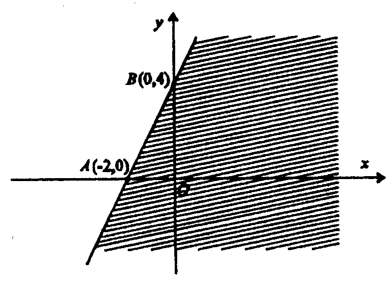
Црт.1

