1. ОСНОВНИ ТРИГОНОМЕТРИСКИ РАВЕНКИ
1.1 Решавање на равенката: sin x = a
Основниот агол arc sin α е аголот којшто се содржи во интервалот [-π/2 ; π/2] и чиј синус е еднаков на a, т.е:
arc sin α = xₒ <=> sin xₒ
Општото решение на равенката sin x = a , е

– Равенката sin x = 0 има решение х = kπ.
– Равенката sin x = 1 има решение x = π/2 + 2kπ
– Равенката sin x = -1 има решение x = -π/2 + 2kπ
1.2. Решавање на равенката cos x = а
Основен агол е аголот што се содржи во сегментот [0, π], чиј косинус е еднаков на бројот а, т.е.
arc cos a = xₒ <=> cos xₒ
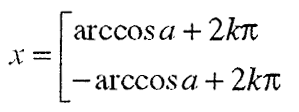
Општото решение на равенката соѕ х = а , е
– Равенката соѕ х = 0 има решение x = π/2 + kπ
– Равенката cos x = 1 има решение x = 2kπ
– Равенката соѕх = -1 има решение x = (2k+1)π
1.3. Решавање на равенката tg x = а
Основниот агол arc tg а е аголот што се содржи во интервалот (– π/2 ; π/2) и чиј тангенс е еднаков на бројот a, т.е.
arc tg a = xₒ <=> tg xₒ
Општото решение на равенката tgx = а , е:
x = arc tg a + kπ
1.4. Решавање на равенката ctg x = а
Основниот агол arc ctg a е аголот што се содржи во интервалот (0, π) и чиј котангенс е еднаков на бројот а, т.е.
arc ctg a = xₒ <=> ctg xₒ
Општото решение на равенката ctg x = a , е
x = arc ctg a + kπ
igonometriski ravenki –
= trigonometriski ravenki =

